Phân tích Toán học “ẩn giấu” đằng sau Bitcoin

Đối với những người mới bắt đầu, một trong những lý do khiến Bitcoin.trở nên khó hiểu chính là: công nghệ phía sau nó đã cho chúng ta một định nghĩa hoàn toàn khác.về khái niệm “quyền sở hữu”. Vậy quyền sở hữu trong Bitcoin là gì? Làm thế nào để tạo ra khóa riêng tư (private key), khóa công khai (public key), chữ ký… để giúp bạn toàn quyền sở hữu Bitcoin?

Tất cả đều được thực hiện bởi các thuật toán khoa học và chính xác. Ngay bây giờ, mời bạn cùng chúng tôi.đi sâu phân tích các phép tính Toán học tạo nên thành công của Bitcoin. Riêng đối với những người không có niềm đam mê với những con số,.bạn hãy lướt đến phần kết luận ở cuối bài để tìm ra bài học cho riêng mình nhé!

Bitcoin định nghĩa lại khái niệm về “Quyền Sở hữu”

Theo nghĩa truyền thống, để sở hữu một cái gì đó. Ví dụ như sơ hữu một căn nhà, một chiếc xe hay một khoản tiền… có nghĩa là những thứ này thuộc quyền nắm giữ của chúng ta (hoặc một đơn vị đáng tin cậy như ngân hàng).

Tuy nhiên, với Bitcoin, quyền sở hữu lại được thể hiện một cách hoàn toàn khác. Bitcoin là phi tập trung và không một ai hay một tổ chức nào có khả năng nắm giữ nó trong tay. Những đồng tiền Bitcoin (BTC) này tồn tại dưới dạng các bộ hồ sơ được phân phối trên một cuốn sổ kế toán gọi là chuỗi khối (blockchain). Bản sao của dữ liệu sẽ được chia sẻ cho các mạng lưới máy tính chủ động kết nối với nó.

Hiểu một cách đơn giản, khi “sở hữu” 1 Bitcoin có nghĩa là bạn có một hồ sơ lưu trữ 1 BTC. trên blockchain và bạn toàn quyền chuyển nhượng quyền sở hữu hồ sơ này.cho một người khác nếu bạn nắm giữ mã khóa công khai (public) và khóa private ECDSA. Vậy cặp mã khóa này có nghĩa là gì? Và tại sao cặp mã khóa này giúp Bitcoin an toàn?

Chúng ta sẽ cùng đi sâu phân tích nhé!

ECDSA là viết tắt của Elliptic Curve Digital Signature Algorithm –.một thuật toán chữ ký điện tử được tạo nên từ đường cong Elliptic. Theo đó, ECDSA kết hợp 1 đường cong elliptic và 1 trường hữu hạn để tạo ra chữ ký (sign) nhằm xác nhận phê duyệt chuyển nhượng quyền sở hữu BTC. Chữ ký này buộc phải đảm bảo 2 yếu tố: chữ ký độc quyền và mọi người có thể xác minh tính xác thực của chữ ký đó.

Nhìn chung, thuật toán ECDSA có những công thức riêng biệt.trong việc tạo ra chữ ký và xác minh giao dịch. Mỗi công thức là một thuật toán riêng. Các thuật toán tạo ra chữ ký này sử dụng các khóa riêng (private key), và quá trình xác minh dùng khóa công khai (public key). Để hiểu hơn về vấn đề này, chúng ta sẽ cùng nhau phân tích các ví dụ cụ thể.

Tuy nhiên, trước tiên, hãy cùng nhau tìm hiểu nhanh về 2 yếu tố tạo ra chữ ký, bao gồm: đường cong Elliptic và các trường hữu hạn.

Từ A-Z về đường cong Elliptic

Đường cong Elliptic là một phương trình có dạng:

y ² = x ³ + ax + b

Với phiên bản của Bitcoin, các giá trị a,b được tính là: a = 0 và b = 7. Khi biểu diễn trên biểu đồ, chúng được thể hiện như sau:

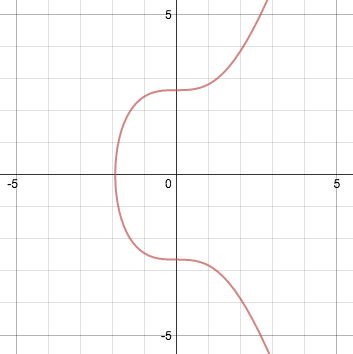
Mỗi đường cong Elliptic giải thích rất nhiều điều ý nghĩa. Ví dụ, một đường thẳng nằm xéo giao với đường cong tại 2 điểm.thì chúng sẽ luôn giao với đường cong tại một điểm thứ 3. Một tính chất khác là: một đường thẳng nằm xéo so với đường cong.và giao với đường cong tại 1 điểm thì.chúng sẽ tiếp tục giao với đường cong ấy tại một điểm thứ 2.

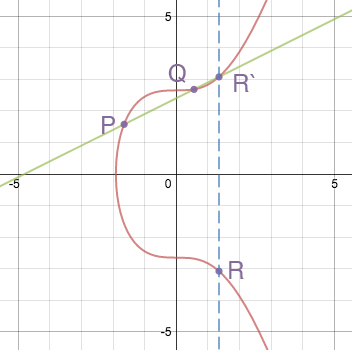
Dựa vào các đặc tính này, chúng ta có thể xác định 2 phép toán:.Cộng Điểm và Nhân đôi Điểm.

Trước tiên là phép Cộng Điểm được tính bằng công thức: P + Q = R. Công thức này được tính bằng dựa trên điểm giao nhau thứ 3 là R’. Để hiểu hơn về công thức này, chúng ta sẽ cùng nhau.biểu diễn phương trình trên trục số như sau:

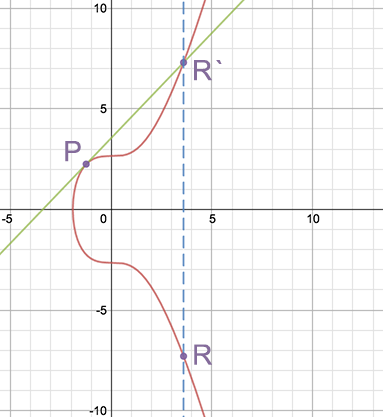
Tương tự, phép Nhân đôi Điểm được tính như sau: P + P = R. Theo đó, R’ được tính bằng cách nhân đôi điểm P và R.sẽ được tìm ra bằng cách đối xứng R’ thông qua trục X. Để hiểu rõ hơn về công thức này, mời bạn tham khảo:

2 phép tính Cộng Điểm và Nhân đôi Điểm đã được dùng để tạo nên phép Nhân Vô Hướng với công thức: R=a*P. Theo đó, R được xác định bằng cách thêm nhiều lần điểm P với chính nó. Ví dụ:

R = 7P
R = P + (P + (P + (P + (P + (P + P)))))

Quá trình nhân vô hướng có thể được đơn giản hóa.bằng cách kết hợp phép Cộng Điểm và Nhân đôi Điểm. Ví dụ:

R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P)

Theo công thức R = P + 2 (P + 2P) thì 7P đã được chia thành 2 bước: nhân đôi điểm 2 bước cộng điểm.

Những điều cần biết về Trường Hữu hạn

Đối với ECDSA, một trường hữu hạn được hiểu như là một tổ hợp (có giới hạn) các số nguyên dương được xác định trước và toàn bộ các phép tính sẽ nằm trong phạm vi những con số chúng ta đã có. Bất kỳ con số nào ngoài tổ hợp này sẽ được quy hoạch về trong tổ hợp.

Cách đơn giản nhất để thể hiện quá trình đưa các con số ngoài tổ hợp về trong phạm vi tổ hợp chính là phép tìm số dư (hay còn gọi là phép modulus (mod)). Ví dụ chúng ta phân tích phép chia 9/7 sẽ ra con số dư là 2.

9 mod 7 = 2

Theo ví dụ trên, trường hữu hạn của ta là modulo 7. Tất cả các phép toán mod 7 đều sẽ cho một con số dư nằm trong phạm vi tổ hợp từ 0-6.

Sự kết hợp của đường cong Elliptic và Trường Hữu hạn

Như đã nói ở trên, ECDSA kết hợp các đường cong Elliptic với các thông số nằm trong một trường hữu hạn. Chính điều này đã làm thay đổi đáng kể các hình dạng của nó nhưng vẫn bảo toàn phương trình cơ bản và tính chất đặc biệt của nó. Một phương trình tương tự nằm trong trường hữu hạn của modulo 67 sẽ có hình dạng như thế này:

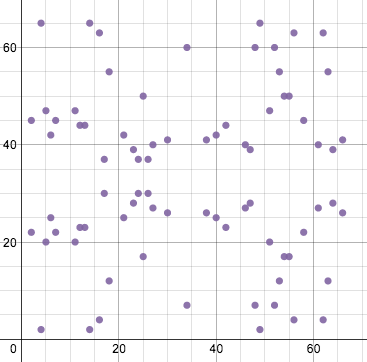
Lúc này, tất cả trở thành một tập hợp điểm. Trong đó mọi giá trị x và y đều là số nguyên, nằm trong phạm vi tổ hợp số từ 0-66.

Xét về mặt trực quan, phép cộng điểm và nhân đôi điêm theo cách biểu diễn này sẽ có hơi khác nhau một chút. Đường vẽ trên đồ thị này sẽ quấn quanh hướng ngang và dọc, giống như trong một trò chơi các tiểu hành tinh, và vẫn duy trì độ dốc. Vì vậy, nếu cộng điểm (2, 22) và (6, 25) thì đồ thị sẽ trông như thế này:

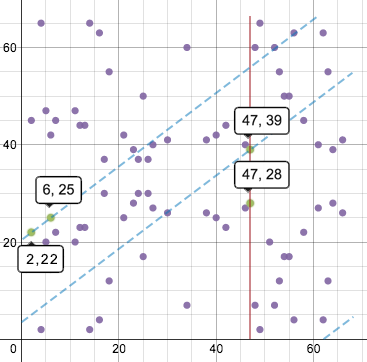
Quay trở lại phân tích ECDSA và Bitcoin

Giao thức Bitcoin chọn một tập các tham số cho các đường cong elliptic và trường hữu hạn của nó để áp dụng cố định cho tất cả người dùng giao thức. Các thông số này bao gồm: các phương trình, modulo số nguyên tố của trường này, và một điểm cơ sở nằm trên đường cong. Bậc của điểm cơ sở không được lựa chọn độc lập mà là một hàm của nhiều thông số khác. Chúng có thể được xem như số lần điểm đó có thể được cộng vào chính nó cho tới khi độ dốc của nó là vô hạn (tức là một đường thẳng đứng). Các điểm cơ sở được lựa chọn sao cho bậc là một số nguyên tố lớn.

Đối với điểm cơ sở, modulo nguyên tố, và bậc, Bitcoin thường sử dụng các con số rất lớn. Tất cả các ứng dụng thực tế của ECDSA đều sử dụng các giá trị rất lớn. An ninh của các thuật toán bảo mật dựa trên các giá trị lớn. Do đó rất khó có ai đảo ngược hoặc tấn công hàng rào bảo mật của Bitcoin bằng các phép thử tấn công lần lượt.

Đối với Bitcoin:

Phương trình đường congElliptic là: y ² = x ³ + 7

Modulo nguyên tố = 2²⁵⁶ – 2³² – 2⁹ – 2⁸ – 2⁷ – 2⁶ – 2⁴ – 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Điểm cơ sở = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Bậc của điểm = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Câu hỏi đặt ra là: ai đã chọn những con số này và tại sao họ lại lựa chọn? Đã có rất nhiều nghiên cứu, và một lượng kha khá những thuyết âm mưu xung quanh việc lựa chọn các thông số nêu trên. Tuy nhiên, sau tất cả, số đông các nghiên cứu đều đều chỉ ra là có một phương pháp backdoor để tìm ra khóa private. Phương pháp đặc biệt này có tên là secp256k1. Chúng là một phần đường cong elliptic trên trường vô hạn đã được đề xuất để sử dụng trong ngành mật mã.

Khóa Private và khóa Public là gì?

Ngay bây giờ, chúng ta sẽ cùng tìm hiểu nhanh về khóa công khai (Public key) và khóa riêng tư (private key). Sau đó chúng ta sẽ phân tích sự liên quan mật thiết của chúng.

Hiểu một cách đơn giản, trong ECDSA, khóa riêng tư là một dãy số ngẫu nhiên, không ai có thể đoán được. Dãy số này nằm giữa số 1 và bậc của điểm. Trong khi đó, khóa công khai được tạo nên từ khóa riêng bằng cách nhân vô hướng khóa riêng tư với điểm cơ sở. Phương trình này được biểu diễn như sau:

Khóa public = khóa private * điểm cơ sở

Phương trình này cho thấy: số lượng tối đa khóa private (các địa chỉ Bitcoin) là bằng bậc của điểm.

Trong một trường liên tục, chúng ta có thể vẽ đường tiếp tuyến và xác định khóa public trên đồ thị. Tuy nhiên, có một số phương trình có thể thực hiện điều tương tự trong bối cảnh trường hữu hạn. Từ phép cộng điểm p + q để tìm ra r được xác định như sau:

c = (q_y – p_y) / (q_x – p_x)
r_x = c² – p_x – q_x
r_y = c (p_x – r_x) – p_y

Đồng thời, từ phép nhân đôi điểm p, chúng ta có thể tìm ra r như sau:

c = (3p_x² + a) / 2p_y
r_x = c² – 2p_x
r_y = c (p_x – r_x) – p_y

Trên thực tế, quá trình tính toán khóa public được chia thành các phép nhân đôi điểm và phép cộng điểm  bắt đầu từ điểm cơ sở.

Để có cái nhìn trực quan về về đề này, chúng ta hãy tham khảo một số ví dụ với các con số nhỏ dưới đây:

Phương trình: y ² = x ³ + 7 (a = 0 và b = 7)
Modulo nguyên tố: 67
Điểm cơ bản: (2, 22)
Bậc của điểm: 79
Khóa riêng: 2

Đầu tiên, hãy cùng nhau tìm khóa public với khóa private có giá trị = 2. Ngay bây giờ, chúng ta chỉ cần thực hiện phép toán nhân đôi điểm một lần từ điểm cơ sở:

c = (3 * 2² + 0) / (2 * 22) mod 67
c = (3 * 4) / (44) mod 67
c = 12 / 44 mod 67

Hãy dừng lại để xem xét một vấn đề nhỏ: Làm sao để thực hiện một phép chia với số dư thuộc trường hữu hạn – nơi kết quả phép chia phải luôn là số nguyên? Với trường hợp này, chúng ta phải làm thêm một phép nhân với nghịch đảo (nếu bạn quan tâm, có thể ở đây và ở đây). Trong trường hợp hiện tại, bạn sẽ phải tin tưởng chúng tôi khi viết rằng:

44^-1 = 32

Bây giờ, chúng ta sẽ tiếp tục với các phép tính:

c = 12 * 32 mod 67
c = 384 mod 67
c = 49

r_x = (49² – 2 * 2) mod 67
r_x = (2401 – 4) mod 67
r_x = 2397 mod 67
r_x = 52

r_y = (49 * (2 – 52) – 22) mod 67
r_y = (49 * (-50) – 22) mod 67
r_y = (-2450 – 22) mod 67
r_y = -2472 mod 67
r_y = 7

Như vậy, từ kết quả trên, khóa public của chúng ta tương ứng với điểm (52, 7). Tất cả chỉ để tính cho khóa riêng bằng 2!

Nhìn chung, phép toán đi từ khóa private tính ra khóa public là một phép toán khá đơn giản và có thể được tính trên máy tính.  Tuy nhiên, nếu muốn làm ngược lại – đi từ khóa public sang khóa private lại là một phương án không khả thi. Đơn giản vì các thông số trong mật mã elliptic là rất lớn.

Nói cách khác, việc đi từ khóa private để tính ra khóa public là chuyến đi một chiều và không thể đảo ngược.

Thông thường, khóa public thường được đại diện bởi một chuỗi thập lục phân. Đợi đã! Làm thế nào để chúng ta nhận được từ một điểm trên mặt phẳng, được mô tả bởi hai con số, để ra một số duy nhất? Trong một khóa public không được nén, hai số 256-bit đại diện cho các tọa độ x và y được đính với nhau trong một chuỗi ký tự dài. Chúng ta cũng có thể tận dụng lợi thế của tính đối xứng của các đường cong elliptic để tạo ra một khóa public nén, chỉ bằng cách giữ giá trị x và ghi nhận nửa nào của đường cong mà điểm đó nằm trên. Từ phần thông tin này, chúng ta có thể phục hồi cả hai tọa độ.

Cách tạo ra chữ ký phê duyệt một số dữ liệu với khóa Private

Giả sử chúng ta đang có một cặp khóa private và khóa public, quá trình tạo ra chữ ký phê duyệt dữ liệu sẽ được diễn ra như sau:

Bạn biết đấy, các dữ liệu có thể có độ dài bất kỳ. Thông thường, quá trình tạo ra chữ ký sẽ bắt đầu bằng bước băm (hash) dữ liệu để tạo ra một số có chứa cùng một số bit (256) như bậc của điểm của đường cong. Tuy nhiên, để giúp bạn dễ hiểu hơn, chúng ta sẽ bỏ qua bước băm và chỉ ký dữ liệu thô z. Nếu gọi G là điểm cơ sở, n là bậc của điểm và d là khóa private. Quá trình tạo ra chữ ký sẽ trải qua 5 bước:

• Bước 1: Chọn một số nguyên ktrong giới hạn giữa 1 và n – 1.
• Bước 2: Tính điểm (x, y) = k* G bằng cách sử dụng phép nhân vô hướng
• Bước 3: Tìm r = x mod n. Nếu r = 0,bạn cần quay lại bước 1.
• Bước 4: Tìm s = (z + r * d) / k mod n. Nếu s = 0, bạn sẽ tiếp tục lại bước 1
• Bước 5: Tạo ra chữ ký là cặp (r, s)

Lưu ý: Trong bước 1, bạn phải chọn k ngẫu nhiên, không được lặp lại trong bất kỳ chữ ký nào và k không thể bị bên thứ ba nào đó đoán ra. Nếu bên thứ ba phát hiện ra k, họ hoàn toàn có thể tìm ra khóa private trong bước 4 (đơn giản vì s, z, r, k và n đều được biết). Để hiểu hơn về quá trình tấn công khi bên thứ ba đoán ra k, bạn có thể đọc về một trường hợp tấn công tương tự tại đây.

Để hiểu hơn về công thức trên, mời bạn tham khảo ví dụ sau:

Giả sử, chúng ta chọn dữ liệu là số 17 với các biến số:

z = 17
n = 79
G = (2, 22)
d = 2

Bước 1: chọn 1 số k ngẫu nhiên: k = rand (1, n – 1)

k = rand (1, 79 – 1)
k = 3 (dù số này không thực sự ngẫu nhiên nhưng chúng sẽ giúp chúng ta phân tích quá trình tạo ra chữ ký một dễ dàng và dễ hiểu)

Bước 2: Tính điểm. Quá trình này sẽ được tính theo cách xác định khóa public. Tuy nhiên, để ví dụ trở nên ngắn gọn súc tích,.chúng ta sẽ bỏ qua phép cộng điểm và nhân đôi điểm số học.

(x, y) = 3G
(x, y) = G + 2G
(x, y) = (2, 22) + (52, 7)
(x, y) = (62, 63)
x = 62
y = 63

Bước 3: Tìm r:

r = x mod n
r = 62 mod 79
r = 62

Bước 4: Tìm s:

s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141/3 mod 79
s = 47 mod 79
s = 47

Bước 5: Chúng ta thu được chữ ký:

 (r, s) = (62, 47)

Tương tự như các khóa private và khóa public,.chữ ký này thường được đại diện bởi một chuỗi thập lục phân.

Sử dụng chữ ký để xác minh giao dịch

Lúc này đây, chúng ta đã có dữ liệu và chữ ký để xác minh dữ liệu đó. Khi một bên thứ ba nào đó nắm giữ khóa Public của chúng ta,.họ hoàn toàn có khả năng nhận được dữ liệu và chữ ký mà chúng ta gửi. Họ cũng có thể xác minh chắc chắn rằng chúng ta chính là những người gửi dữ liệu đó.

Gọi Q là khóa công khai với các biến được xác định như trước đây. Quá trình xác minh chữ ký sẽ được thể hiện như sau:

• Bước 1: Xác minh r và s nằm trong phạm vi 1 và n – 1.
• Bước 2: Tính w = s^-1 mod n
• Bước 3: Tính u = z * w mod n
• Bước 4: Xác định v = r * w mod n
• Bước 5: Tính điểm (x, y) = uG + vQ
• Bước 6: Xác minh r = x mod n.

Trong trường hợp phương trình này không đúng thì chữ ký không hợp lệ.

Lúc này, câu hỏi đặt ra là: tại sao có thể dùng các bước trên đây.để xác minh chữ ký? Hãy tìm hiểu thêm thông tin chi tiết ở đây.

Quay trở lại với quy trình xác minh chữ ký ban đầu,.để hiểu rõ hơn về các bước nêu trên, mời bạn tham khảo ví dụ sau:

Giả sử chúng ta có:

z = 17

(r, s) = (62, 47)

n = 79

G = (2, 22)

Q = (52, 7)

Bây giờ, chúng ta sẽ tuần tự xác minh theo các bước từ 1 đến 6

• Bước 1: xác minh r và s nằm trong khoảng từ 1 đến n-1

Ta có:

r: 1 <= 62 <79
s: 1 <= 47 <79

Như vậy, r và s thỏa mãn bước 1.

• Bước 2: Tính giá trị của w

w = s^-1 mod n
w = 47^-1 mod 79
w = 37

• Bước 3: Tính giá trị của u:

u = zw mod n
u = 17 * 37 mod 79
u = 629 mod 79
u = 76

• Bước 4: Tính giá trị của v:

v = rw mod n
v = 62 * 37 mod 79
v = 2294 mod 79
v = 3

• Bước 5: Tính điểm (x, y):

(x, y) = uG + vQ

Tiếp theo, chúng ta hãy tách uG và vQ sau đó tính toán.dựa trên phép Cộng điểm và phép Nhân đôi điểm:

uG = 76G
uG = 2(38G)
uG = 2( 2(19G) )
uG = 2( 2(G + 18G) )
uG = 2( 2(G + 2(9G) ) )
uG = 2( 2(G + 2(G + 8G) ) )
uG = 2( 2(G + 2(G + 2(4G) ) ) )
uG = 2( 2(G + 2(G + 2( 2(2G) ) ) ) )

Việc sử dụng phép nhóm lại như trên giúp chúng ta giảm từ 75 phép cộng điểm liên tục xuống còn.6 lần thực hiện phép nhân đôi điểm và 2 lần thực hiện phép cộng điểm. Khi các con số càng lớn thì những thủ thuật này.càng giúp chúng ta rút ngắn thời gian tính toán.

Bây giờ, chúng ta sẽ cùng tính toán nhé!

uG = 2( 2(G + 2(G + 2( 2( 2(2, 22) ) ) ) ) )
uG = 2( 2(G + 2(G + 2( 2(52, 7) ) ) ) )
uG = 2( 2(G + 2(G + 2(25, 17)  ) ) )
uG = 2( 2(G + 2( (2, 22) + (21, 42) ) ) )
uG = 2( 2(G + 2(13, 44) ) )
uG = 2( 2( (2, 22) + (66, 26) ) )
uG = 2( 2(38, 26) )
uG = 2(27, 40)
uG = (62, 4)

Tiếp theo, chúng ta sẽ cùng tính cho vQ:

vQ = 3Q
vQ = Q + 2Q
vQ = Q + 2(52, 7)
vQ = (52, 7) + (25, 17)
vQ = (11, 20)

Cuối cùng, hãy gộp chúng lại với nhau:

(x, y) = uG + vQ
(x, y) = (62, 4) + (11, 20)
(x, y) = (62, 63)

Cuối cùng, chúng ta xác minh tính đúng đắn của chữ ký bằng phương trình r = x mod n

r = x mod n
62 = 62 mod 79
62 = 62

Như vậy, chữ ký của chúng ta nhận được hoàn toàn là hợp lệ!

Kết luận

Từ các phương trình toán học nêu trên, ta thấy: Khóa public và khóa private của Bitcoin luôn có một mối quan hệ sâu sắc. Và bạn biết đấy, đằng sau những chữ ký và xác minh đơn giản là những phép toán phức tạp. Nhất là các thông số liên quan đến những con số  256-bit thì độ phức tạp lại càng cao.

Và có một điều quan trọng chúng ta phải thừa nhận rằng: các ứng dụng thông minh của các thủ thuật toán học đơn giản nhất.hoàn toàn có thể tạo ra những “cái bẫy” một chiều để bảo vệ quyền sở hữu Bitcoin. Qua đó, chúng ta có thể tin vào sức mạnh của hệ thống.và luôn cẩn thận bảo vệ các thông tin khóa private để giữ an toàn cho đồng tiền của mình.

Tất cả những công thức nêu trên giải thích lý do tại sao nhiều người nhận định rằng Bitcoin được “sự ủng hộ của toán học.”

Hi vọng, bài viết này đã đem đến cho bạn nhiều kiến thức bổ ích.và giúp bạn tự tin thử các phép toán (hãy dùng máy tính số học modular để tính toán nhanh hơn nhé). Và mong rằng, khi hiểu sâu về các bước của việc ký kết cũng như xác minh dữ liệu bằng tay.sẽ giúp chúng ta hiểu sâu sắc hơn về mật mã đại diện cho hình thức sở hữu độc đáo,.riêng biệt của đồng tiền mã hóa Bitcoin.

***

Cảm ơn anh Steven Phelps đã giúp đỡ chúng tôi thực hiện bài viết này!

Nguồn: The Math behind Bitcoin – Chain.com

Bản dịch gốc của ông Phil Trịnh đã được BitcoinVN News biên tập lại